

We note that for scenario (1), Fisher's method for combining p-values is commonly used. In this paper, we focus on scenario (2), which is a common situation in genetic studies. Statistical methods can differ depending on the scenario: when (1) test statistics are unknown but only p-values are available, (2) test statistics are known but data are not available, or (3) actual data are available. There exist several approaches for combining information from multiple studies. The meta-analysis has also become a useful tool for many applications of bioinformatics, such as neuroimage processing and expression quantitative trait loci analysis. In the field of genetics, the meta-analysis has become a popular way of aggregating information from multiple genome-wide association studies (GWASs) in order to increase statistical power while controlling for the rate of false positive findings. The meta-analysis is a tool for pooling information from multiple independent studies. Finally, we apply both methods to the Wellcome Trust Case Control Consortium data and demonstrate that the two methods can give distinct results in certain study designs.

We examine the connection between the two methods both analytically and empirically and show that their resulting statistics become equivalent under certain assumptions. We demonstrate that the each method is optimized for a unique goal, which gives us insight into the optimal weights for the weighted sum of z-scores method.
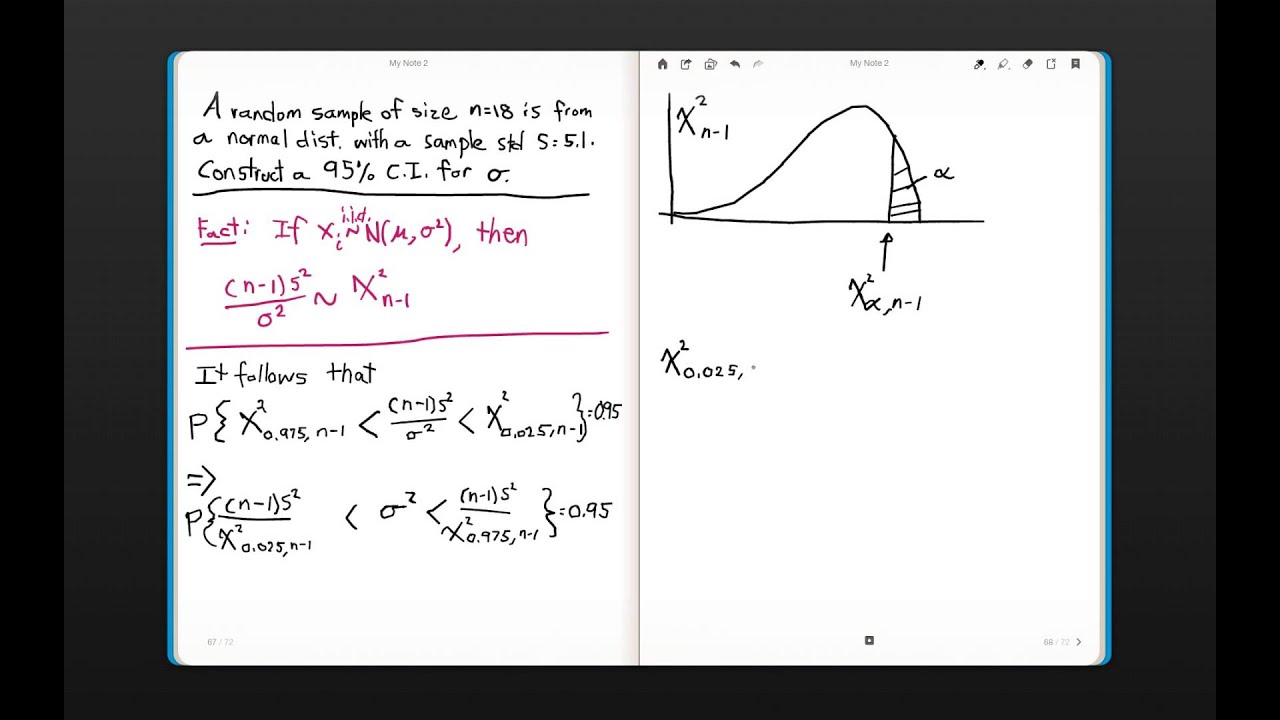
In this paper, we investigate the optimal characteristics of the two methods and show the connection between the two methods. Although previous studies have shown that the two methods perform similarly, their characteristics and their relationship have not been thoroughly investigated. A commonly used approach for meta-analysis is the fixed effects model approach, for which there are two popular methods: the inverse variance-weighted average method and weighted sum of z-scores method. If all are unique, then counts the number of unique values, and counts the number of samples.įor example, if values are drawn from the same distribution, then we can treat this set as an unweighted sample, or we can treat it as the weighted sample with corresponding weights, and we should get the same results.The meta-analysis has become a widely used tool for many applications in bioinformatics, including genome-wide association studies. If all of the are drawn from the same distribution and the integer weights indicate frequency of occurrence in the sample, then the unbiased estimator of the weighted population variance is given by The standard deviation is simply the square root of the variance above. The degrees of freedom of the weighted, unbiased sample variance vary accordingly from N − 1 down to 0. The unbiased estimator of a weighted population variance (assuming each is drawn from a Gaussian distribution with variance ) is given by : While this is simple in unweighted samples, it is not straightforward when the sample is weighted.
In normal unweighted samples, the N in the denominator (corresponding to the sample size) is changed to N − 1. Where, which is 1 for normalized weights.įor small samples, it is customary to use an unbiased estimator for the population variance. The biased weighted sample variance is defined similarly to the normal biased sample variance: When a weighted mean is used, the variance of the weighted sample is different from the variance of the unweighted sample. Typically when a mean is calculated it is important to know the variance and standard deviation about that mean.


 0 kommentar(er)
0 kommentar(er)
